Seminario su:

SCAVI, PENDII E OPERE DI SOSTEGNO 

Stima dei cedimenti indotti da scavi a cielo  aperto e rischio di danno agli edifici 

 

  Giovanni Vannucchi

Dipartimento di Ingegneria Civile e Ambientale – Università di Firenze            Venerdì 29 giugno 2018, Aula Magna – ISIS Leonardo da Vinci

Via del Terzolle 91 ‐ Firenze

 

 

Indice:

3.Stima dei cedimenti indotti da uno scavo a cielo aperto sostenuto da un diaframma 9

3.1. Metodo di Peck (1969)	12
3.2. Metodo di Bauer (1984)	13
3.3. Metodo di Bowles (1988)	14
3.4. Metodo di Clough e O’Rourke (1990)	15
3.5. Metodo di Clough e altri (1989)	16
3.6. Metodo di Hsieh e Ou (1998)	18
3.7. Metodo di Bryson e Zapata‐Medina (2012)	20
4.            Stima degli effetti tridimensionali	22
5.            Rischio di danno agli edifici	24
Riferimenti bibliografici	30

 

1. Introduzione

La necessità di sfruttare il sottosuolo per risolvere problemi di viabilità e di trasporto nelle aree urbane, con la realizzazione di parcheggi interrati, di gallerie e di stazioni per linee metropolitane e ferroviarie, ha molto incrementato la realizzazione di scavi a cielo aperto e in sotterraneo.

Foto 1 – Scavo per la realizzazione della stazione dell’AV a Firenze

Poiché ogniqualvolta che si interviene modificando lo stato di tensione nel sottosuolo si producono deformazioni e cedimenti, la realizzazione di tali opere comporta necessariamente un rischio per le infrastrutture e per le costruzioni esistenti, tanto più elevato nei centri storici delle città italiane, ove il tessuto urbano ha spesso valore storico‐monumentale ma anche grande fragilità.

Lo studio rigoroso dei cedimenti indotti da scavi a cielo aperto è molto difficile e incerto, poiché implica la conoscenza di dettaglio delle condizioni stratigrafiche e geotecniche, la precisa successione e la tempistica delle fasi di realizzazione dell’opera, l’utilizzazione di leggi costitutive complesse, i cui parametri sono di difficile e incerta determinazione, l’impiego di metodi di calcolo numerico. Un approccio di tal genere richiede la definizione di un modello geotecnico che può essere calibrato in base ai dati derivanti da un monitoraggio dell’opera in costruzione, ma è difficilmente utilizzabile in fase di progetto.

È tuttavia possibile ricorrere a metodi semi‐empirici, basati sull’osservazione del comportamento di numerose opere in vera grandezza, allo scopo di ottenere una stima preliminare, approssimata ma realistica, del cedimento e quindi del rischio associato.

Gli scavi a cielo aperto in ambiente urbano sono di norma sostenuti da palancole metalliche o da diaframmi in c.a. a sbalzo o più frequentemente con uno o più ordini di vincoli (tiranti o puntoni). I cedimenti e gli spostamenti orizzontali del terreno a monte della struttura di sostegno sono strettamente dipendenti dai movimenti di rototraslazione rigida e di deformazione elastica della parete verticale, i quali a loro volta dipendono da moltissimi fattori quali:

• condizioni stratigrafiche, geotecniche e idrauliche del sito,
• rigidezza della parete,
• tecnica di scavo,
• fasi di esecuzione e la loro durata,
• rigidezza, numerosità, disposizione, tecnica di messa in opera e precarico delle strutture di contrasto,
• geometria dello scavo (altezza, profondità di infissione, forma e dimensioni dell’area di scavo), –      qualità della mano d’opera, etc…

In particolare in presenza di falda, se la struttura di sostegno non è immorsata in uno strato impermeabile, lo scavo e la conseguente estrazione di acqua determina un moto di filtrazione discendente all’esterno e ascendente all’interno dell’area di scavo. A tergo della paratia le pressioni interstiziali si riducono, mentre le tensioni efficaci crescono e producono deformazioni di compressione e cedimenti. All’interno dell’area di scavo, al contrario, le pressioni interstiziali crescono e le tensioni efficaci si riducono. Oltre al rischio di instabilità idrodinamica (sifonamento), la riduzione delle tensioni efficaci determina una riduzione della resistenza passiva e della rigidezza del terreno con conseguenti spostamento del tratto interrato del diaframma verso l’interno dello scavo.

A parità di condizioni geometriche, idrauliche e geotecniche, la tecnica costruttiva, la tempistica e la successione delle fasi realizzative dell’opera di sostegno giocano un ruolo importante sui movimenti e cedimenti finali. In particolare la tecnica costruttiva più classica (metodo bottom‐down) prevede la realizzazione delle strutture di sostegno perimetrali, poi dello scavo per fasi e con più livelli di vincoli provvisori (tiranti e/o puntoni), infine la costruzione dal basso verso l’alto dell’opera e la progressiva sostituzione dei vincoli provvisori con gli impalcati. Una tecnica costruttiva alternativa consiste nella messa in opera degli impalcati definitivi via via che procede lo scavo, dall’alto verso il basso (metodo top‐down), lasciando solo delle aperture per l’estrazione del terreno scavato. Procedendo in tal modo si riducono gli spostamenti finali.

Foto 3 – Tecnica costruttiva top‐down

I cedimenti e gli spostamenti finali sono inoltre molto influenzati dalle capacità della mano d’opera di eseguire correttamente e tempestivamente le diverse operazioni costruttive, come ad esempio il ritardo nella messa in opera dei vincoli (tiranti e/o puntoni), la non perfetta verticalità delle strutture di sostegno (pali, palancole e/o pannelli), la cattiva esecuzione dei giunti, etc. …

I metodi di calcolo delle paratie possono ricondursi a tre tipologie, di complessità crescente:

1. I tradizionali e collaudati metodi all’equilibrio limite, che assumono un comportamento rigido‐perfettamente plastico del terreno, ovvero schematizzano la risposta del terreno con diagrammi limite di pressione attiva e passiva, quest’ultima ridotta dall’applicazione di un coefficiente di sicurezza;
2. I metodi a molle indipendenti, tipo Winkler, con cui è possibile tenere conto di leggi costitutive non lineari, anche elasto‐plastiche, e quindi della successione delle fasi di realizzazione dell’opera;
3. I metodi che modellano il terreno come mezzo continuo, elastico, elastico non lineare o elasto‐plastico.

 

Soltanto i metodi di tipo 3, implementati in programmi di calcolo alle differenze finite o agli elementi finiti, sono in grado di calcolare le deformazioni del terreno e quindi i cedimenti e gli spostamenti orizzontali a monte della struttura di sostegno. Tuttavia, affinché il risultato possa essere affidabile, è necessario che il modello geotecnico sia dettagliato e corrispondente alla realtà fisica, e ciò è talvolta impossibile o comunque difficile da verificare con sicurezza, e assai costoso, poiché possono essere necessarie indagini geotecniche in sito e di laboratorio molto approfondite e spesso inusuali. Si deve sempre avere presente che un risultato molto preciso ma non accurato è pericoloso, poiché può ingenerare un falso senso di sicurezza. Pertanto i metodi che modellano il terreno come mezzo continuo trovano la loro massima utilità:

1. nella fase più avanzata di progettazione di scavi di grande impegno ed importanza per le quali sia giustificata una approfondita indagine geotecnica,
2. per modificare la previsione del comportamento in corso d’opera sulla base di dati di monitoraggio che consentano la calibrazione del modello geotecnico,
3. per controlli e verifiche post operam, d) per analisi parametriche e di sensibilità.

Nelle fasi preliminari di progettazione, e comunque per un confronto ed una validazione di risultati ottenuti per via numerica, è opportuno riferirsi alle basi dati sperimentali relativi all’osservazione di opere realizzate in passato, opportunamente catalogati e normalizzati, ed ai metodi empirici e agli abachi di progetto da essi derivati. Molto spesso in tali abachi i movimenti della parete sono correlati con il fattore di sicurezza rispetto al sollevamento del fondo.

 

2. Stima dei cedimenti indotti dallo scavo delle trincee per la costruzione dei pannelli di diaframma

Molto spesso gli scavi sono sostenuti da pareti diaframma in c.a costituiti da pannelli affiancati^[1]. La realizzazione delle pareti diaframma è articolata nelle seguenti fasi:

1. scavo dei pannelli pari (o dispari) a sezione obbligata in profondità con benna mordente e/o con idrofresa, previa stabilizzazione delle pareti con fango bentonitico;
2. posa in opera della gabbia di armatura preassemblata e di eventuali casseri recuperabili per la formazione di giunti;

• getto del calcestruzzo nello scavo, dal basso verso l’alto (sistema contractor), che si sostituisce al fango bentonitico:

1. ripetizione delle operazioni per i pannelli dispari (o pari).

Durante lo scavo delle trincee per la costruzione dei pannelli, a causa della sostituzione del terreno asportato con fango bentonitico, il cui peso di volume è inferiore a quello del terreno, si determina una riduzione delle tensioni orizzontali totali in prossimità della trincea. Le conseguenti deformazioni laterali causano cedimenti del piano campagna. Il successivo getto del calcestruzzo, il cui peso di volume è superiore a quello del terreno, produce un recupero delle tensioni orizzontali ma solo in misura minima il recupero dei cedimenti. I cedimenti causati dallo scavo delle trincee per la costruzione dei pannelli sono inferiori e interessano una fascia di minore larghezza rispetto ai cedimenti dovuti allo scavo del terreno, ma possono non essere trascurabili. La letteratura tecnica non riporta molti casi documentati di cedimenti indotti dallo scavo delle trincee: Clough e O’Rourke (1990) verificarono che il rapporto fra il cedimento massimo e la profondità della trincea (_v/H_t) è inferiore a 0.15% (Figura 4); Ou e Yang (2000) analizzando i risultati del monitoraggio dei cedimenti indotti dallo scavo delle trincee per la costruzione dei pannelli per una linea ferroviaria a Taipei (Taiwan) trovarono che il massimo cedimento indotto dallo scavo di un singolo pannello era stato 0.05H_t %, che il massimo cedimento cumulato indotto dallo scavo di più pannelli era stato

0.07H_t %,.e che il massimo cedimento indotto dalla realizzazione di tutto il diaframma era stato

0.13H_t %. In Figura 5 sono riportati i profili dei cedimenti del piano campagna osservati da Ou e Yang (2000), e il profilo limite inviluppo secondo Clough e O’Rourke (1990).

 

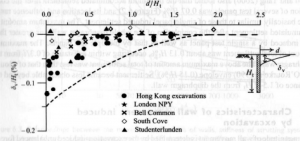
Figura 4 – Inviluppo dei cedimenti del piano campagna causati dallo scavo delle trincee per la costruzione dei diaframmi (Clough e O’Rourke, 1990)

 

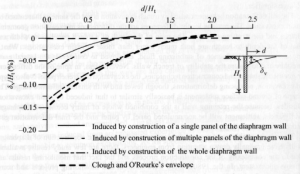
Figura 5 – Profili dei cedimenti indotti dallo scavo di trincee per la costruzione di diaframmi a Taipei (Ou e Yang ,2000)

 

3. Stima dei cedimenti indotti da uno scavo a cielo aperto sostenuto da un diaframma

Il profilo dei cedimenti causati da uno scavo a cielo aperto sostenuto da un diaframma può essere di due tipi (Figura 6):

• profilo a mensola (“spandrel type”), in cui il cedimento massimo in superficie è in corrispondenza della parete, e
• profilo concavo (“concave type”), in cui il cedimento è ad una certa distanza dalla parete.

La forma del profilo dei cedimenti e la deformata della parete dipendono dalla presenza, disposizione, rigidezza e tempi di messa in opera delle strutture di contrasto dei movimenti della parete (tiranti o puntoni):

• Se la parete subisce la maggior parte delle deformazioni prima della messa in opera delle strutture di contrasto, il profilo dei cedimenti e la linea elastica della parete avranno forma a mensola;
• Se invece la maggior parte delle deformazioni si verificano dopo la messa in opera di strutture di contrasto rigide il profilo dei cedimenti e la linea elastica della parete avranno forma concava (Figura 7).

 

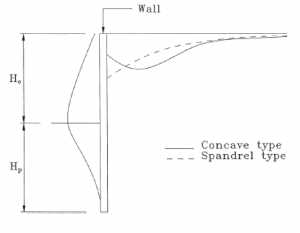
Figura 6 – Forme del profilo dei cedimenti e deformata della parete di sostegno di uno scavo a cielo aperto (da Hsieh e Ou, 1998)

 

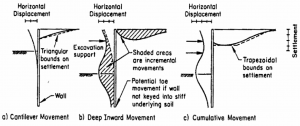
Figura 7 – Profili dei cedimenti dietro le paratie a sostegno di scavi a cielo aperto (Clough e O’Rourke, 1990)

 

In particolare nella prima fase di uno scavo eseguito con la tecnica “bottom‐down”, quando ancora non sono state messe in opera le strutture di contrasto dei movimenti, la parte superiore della parete si deforma a mensola, e i cedimenti a tergo hanno il massimo in corrispondenza della parete e decrescono allontanandosi da essa (“spandrel type”). Con la messa in opera dei diversi livelli di vincolo che impediscono, o comunque limitano molto, gli spostamenti orizzontali del tratto superiore della parete, si manifestano movimenti orizzontali nella parte inferiore della parete, anche al di sotto del piano di scavo, e i cedimenti a tergo presentano un massimo ad una certa distanza dalla parete (“concave type”). Ulteriori movimenti si determinano se e quando i vincoli provvisori (tiranti e/o puntoni) sono rimossi e sostituiti con quelli definitivi, non necessariamente alle stesse quote. In particolare se, come avviene di solito, la rimozione e sostituzione dei vincoli avviene dal basso verso l’alto, nel tempo che intercorre fra la rimozione del livello superiore di vincolo provvisorio e la messa in opera del vincolo definitivo, la struttura ha nuovamente un comportamento a mensola. La deformata e il profilo dei cedimenti finale sono la combinazione e la somma dei movimenti che si sono verificati nelle diverse fasi costruttive.

 

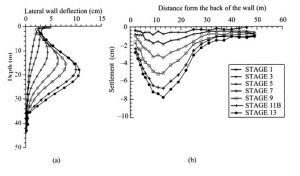
In Figura 8 sono rappresentati i profili della deformata della parete e i corrispondenti profili dei cedimenti a tergo di uno scavo monitorato in corso d’opera a Taipei (Ou et al. 1998). È molto evidente la forte correlazione fra le due serie di curve.

 

Se lo scavo è eseguito con il metodo top‐down tra una fase di scavo e la successiva possono trascorrere lunghi periodi di tempo, durante i quali possono verificarsi deformazioni del terreno per consolidazione e/o per viscosità. Di conseguenza anche la deformata della parete e il profilo dei cedimenti possono modificarsi. Tale fenomeno è messo in evidenza dalle curve di Figura 9, che si riferiscono allo stesso diaframma monitorato di Taipei cui si riferiscono le curve di Figura 8.

 

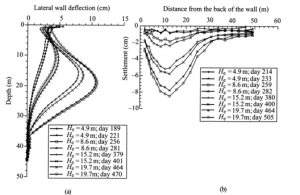
Figura 9 – Effetti del tempo su deformata della parete (a) e profilo dei cedimenti a tergo dello scavo nelle diverse fasi di costruzione di un diaframma (Ou et al., 1998) Molti Autori da un’analisi dei risultati di monitoraggio documentati e disponibili, riferiti ad opere realizzate in luoghi e tempi diversi, con tecnologie diverse, con geometrie diverse, in condizioni diverse, hanno proposto metodi semi‐empirici per stima della forma e dell’entità del profilo dei cedimenti causati da uno scavo a cielo aperto. Tali metodi quanto più sono recenti tanto più sono affidabili e meno cautelativi, perché basati su una casistica più numerosa e varia, e perché nel tempo le tecnologie esecutive sono migliorate. Nel seguito sono brevemente richiamati alcuni di essi.

[1] Le dimensioni usuali dei pannelli sono: spessore S compreso tra 50 e 120 cm, lunghezza L compresa tra 200 e 600 cm).

 

3.1.            Metodo di Peck (1969)

Un contributo storico importante allo studio dei cedimenti causati dagli scavi si deve a Peck (1969), il quale rappresentò graficamente i dati sperimentali relativi a scavi in terreni di varia natura sostenuti da paratie di pali affiancati e disegnò due curve che suddividono il grafico in tre zone: I, II e III, in funzione del tipo di terreno e delle capacità della mano d’opera (Figura 10).

Il metodo di Peck prende in considerazione solo profili a mensola (“spandrel”). Dal grafico si desume che per sabbie e argille di media e elevata consistenza il cedimento massimo (_vm) è inferiore all’1% della profondità di scavo (H_e) e che il bacino dei cedimenti si estende per una distanza dalla parete (d) non superiore a 2 volte la profondità di scavo. Per argille di scarsa consistenza ma con un adeguato coefficiente di sicurezza rispetto al sollevamento del fondo scavo il cedimento massimo (_vm) è compreso tra l’1% e il 2% della profondità di scavo (H_e) e il bacino dei cedimenti si estende per una distanza dalla parete (d) compreso tra 2 e 4 volte la profondità di scavo. Infine per argille di scarsa consistenza e con un insufficiente coefficiente di sicurezza rispetto al sollevamento del fondo scavo il cedimento massimo (_vm) è superiore al 2% della profondità di scavo (H_e) e il bacino dei cedimenti si estende per una distanza dalla parete (d) maggiore di 4 volte la profondità di scavo.

 

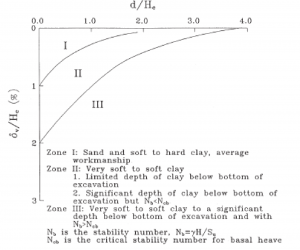
Figura 10 – Cedimenti indotti da scavi a cielo aperto in terreni di vario tipo in funzione della distanza dal bordo (Peck, 1969)

 

Zona I: Sabbia e argilla da molle a dura, mano d’opera di media capacità

Zona II: Argilla da molto molle a molle

1. Piccoli spessori di argilla al di sotto del piano di scavo
2. Significativi spessori di argilla al di sotto del piano di scavo con N_b < N_cb

Zona III: Argilla da molto molle a molle fino a significative profondità sotto il piano di scavo con N_b > N_cb

^H

in cui                          N_b       è il numero di stabilità S_u

N_cb è il numero di stabilità critico per sollevamento del fondo scavo

Il metodo di Peck è piuttosto cautelativo, poiché si riferisce a paratie eseguite prima degli anni ’70. Con strutture di sostegno realizzate con tecnologie più moderne si registrano in genere cedimenti massimi inferiori.

 

3.2.            Metodo di Bauer (1984)

Un metodo semi‐empirico per la stima del profilo parabolico “a mensola” dei cedimenti dovuti ad uno scavo a cielo aperto in terreni sabbiosi è il seguente (Bauer, 1984) (Figura 11):

 

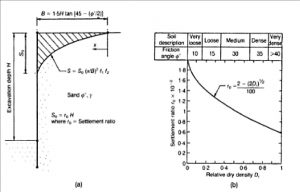
Figura 11 – Metodo di Bauer (1984) per la stima dei cedimenti indotti da scavi in terreni sabbiosi

 x   ²

v  vm   f1 f2

 d 

_vm  r₀ H_e (1)

2         2D R

r ₀ 

100

d 1.5He tan    

 4  2

in cui D_R è la densità relativa della sabbia (0 ≤ D_R ≤1), (d‐x) è la distanza dalla parete, f₁ e f₂ sono coefficienti empirici dipendenti rispettivamente dalla capacità della mano d’opera e dalle difficoltà costruttive (Tabella 1)

Tabella 1 ‐ Coefficienti del metodo di Bauer (19		84)
Capacità della mano d’opera	Ottima	Buona	Media	Scadente
f1	0.8	0.9	1	1.1
Difficoltà costruttive	Nessuna	Medie	Elevate
f2	1	1.02	1.05

 

3.3.            Metodo di Bowles (1988)

Il metodo di Bowles (1988) si applica a profili di cedimento a mensola (“spandrel type”) e si articola nei seguenti passi:

1. stima della deformata (rigida ed elastica) della parete,
2. calcolo del volume dei movimenti laterali del terreno (V_s),
3. stima della distanza di influenza (d) nel modo seguente (Caspe, 1966):

d  H_e  H_d tan^ ^  ^                                                            (2)  4  2

ove sono indicati con:

H_e              la profondità dello scavo,

   l’angolo di resistenza al taglio del terreno, per terreni coesivi H_d = B, con B larghezza dello scavo,

B     ^{      }

per terreni incoerenti H_d     ^tan           

2     4      2

4. stima del cedimento massimo (_vm) in corrispondenza della parete con l’equazione:

^V

_vm  4 _ ^s                                                                                       (3) d

5. si assume che la curva dei cedimenti sia parabolica, e che il cedimento (_v) alla distanza (d – x) dalla parete sia data dall’equazione:

 x  ²

_v  _vm                                                                                      (4)

 d 

La superficie di subsidenza indotta da uno scavo in assenza di cedimenti per consolidazione e la deformata della parete dipendono dagli stessi fattori, come ad esempio la profondità di scavo, la tecnica esecutiva, le strutture di contrasto dei movimenti, etc. Pertanto ha senso stimare i cedimenti in superficie in base all’entità ed alla forma dei movimenti della parete ottenuta da un’analisi delle deformazioni laterali. Se si assume che l’area del bacino dei cedimenti sia approssimativamente eguale all’area della deformata del muro per argille molli in condizioni non drenate

(Milligan, 1983), risulta: _vm  3 V ^s , Bowles (1988) assume invece _vm  4 ^Vs , probabilmente d   d

per ottenere un miglior accordo con le osservazioni dei casi reali

 

3.4.            Metodo di Clough e O’Rourke (1990)

Sulla base dell’osservazione di numerosi casi reali Clough e O’Rourke (1990) suggerirono di assumere per scavi in terreni sabbiosi o in argille consistenti un profilo dei cedimenti triangolare con valore massimo in corrispondenza della parete (profilo a mensola). Nelle Figure 12a e 12b sono rappresentati i profili adimensionalizzati dei cedimenti a tergo di scavi rispettivamente in terreni sabbiosi e in argille consistenti e dure. Per scavi in argilla da molle a mediamente consistente, avendo osservato che il cedimento massimo ha luogo ad una certa distanza dalla parete, essi suggerirono di assumere un profilo dei cedimenti di forma trapezia (Figura 12c). I profili suggeriti sono l’inviluppo di profili reali e pertanto sono da considerarsi cautelativi.

Il cedimento massimo _vm può raggiungere lo 0.3% della massima profondità di scavo H_e in terreni sabbiosi o in argille da consistenti a dure, e fino al 2% di H_e in argille da molli a mediamente consistenti (Figura 13).

Il rapporto fra massimo cedimento (_vm) e massimo spostamento orizzontale della parete (_hm) è in genere compreso tra 0.5 e 1.

 

3.5.            Metodo di Clough e altri (1989)

Il metodo di Clough et al. (1989) è una procedura semi‐empirica per stimare i movimenti causati da uno scavo in argilla in cui lo spostamento orizzontale massimo della parete (_hm) è valutato in funzione del coefficiente di sicurezza rispetto al sollevamento del fondo scavo (FS) e della rigidezza del sistema:

EJ

       h ₄                                                                                (5)

_w   

in cui EJ è la rigidezza flessionale per unità di lunghezza della parete, _w è il peso specifico dell’acqua e h è l’interasse medio delle strutture di contrasto dei movimenti (Figura 14).

Le curve di Figura 14 si riferiscono a condizioni di difficoltà costruttive medie e buona capacità della mano d’opera, e all’ipotesi che la deformata a sbalzo della parete contribuisca poco al movimento totale del muro.

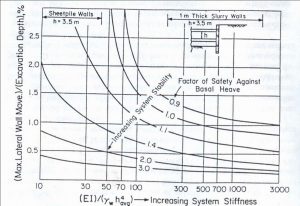
Figura 14 – Stima dei movimenti orizzontali del muro in funzione della profondità di scavo e della rigidezza del sistema (Clough et al., 1989)

Le analisi di stabilità del fondo scavo sono di norma svolte con i tradizionali metodi all’equilibrio limite adottando semplici schemi bi‐dimensionali, trascurando gli effetti della profondità di infissione della parete. In particolare si utilizza in genere il metodo di Terzaghi (1943) rappresentato in Figura 15a, per il quale il coefficiente di sicurezza rispetto al sollevamento del fondo scavo (FS) è:

FS     s u  Nc                        su  Nc                                                (6)

 H_e  q_s s_u  HBe’                Hqs_e  sBu ‘  He

B

in cui B’   T e il fattore di capacità portante vale N_c = 5.7.

L’equazione (6) è utilizzata per il calcolo di FS nel metodo di Clough et al. (1989) rappresentato in Figura 14.

Long (2001) verificò l’applicabilità e l’affidabilità del metodo di Clough e O’Rourke (1990) su oltre 300 casi reali di scavi a cielo aperto sostenuti da muri‐diaframma realizzati in diverse parti del mondo concludendo che:

1. nel caso di opere di sostegno vincolate in terreni consistenti con elevato valore del coefficiente di sicurezza rispetto al sollevamento del fondo scavo (FS), gli spostamenti sono in genere inferiori a quelli previsti dal metodo e in particolare:

‐ il rapporto fra lo spostamento orizzontale massimo e l’altezza dello scavo è di norma:

 ^hm       0.25%

0.05%           

H_e

‐ il rapporto fra lo spostamento verticale massimo e l’altezza dello scavo è di norma:

 ^vm       0.20%

0.00%           

H_e

‐ il sistema di vincolo della struttura (puntoni, tiranti, costruzione top‐down) ha poca influenza sull’entità degli spostamenti laterali;

1. nel caso di strutture di sostegno vincolate in terreni molli fino a profondità superiori a 0.6 H_e, e

immorsate in strati rigidi, con elevato valore di FS, gli spostamenti sono in buon accordo con i valori previsti dal metodo;

1. nel caso di strutture di sostegno vincolate in terreni molli fino a profondità superiori a 0.6 H_e, e immorsate in strati molli con elevato valore di FS, gli spostamenti sono in genere superiori a quelli previsti dal metodo;
2. nel caso di strutture di sostegno vincolate caratterizzate da un basso valore di FS si sono regi‐

 ^hm     3.2% ; strati spostamenti orizzontali elevati, fino a        H_e

1. nel caso di strutture di sostegno non vincolate (a mensola) lo spostamento massimo orizzontale

 ^hm          0.36% è (sorprendentemente) indipendente dalla rigidezza del muro e vale mediamente:       

H_e

Per tenere conto degli effetti dell’infissione della parete al di sotto della profondità di scavo Ukritchon et al. (2003) hanno proposto la seguente equazione modificata per il calcolo del coefficiente di sicurezza rispetto al sollevamento del fondo scavo (Figura 15b):

su  Nc          2 su  H   2su  D  

FS      B    B                                                   (7)

 H_e

in cui il fattore di capacità portante vale N_c = 5.14.

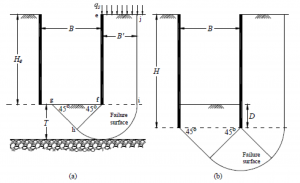
Figura 15 – Coefficiente di sicurezza rispetto al sollevamento del fondo scavo: a) senza infissione del muro (Terzaghi, 1943); e b) con infissione (Ukritchon et al., 2003)

 

3.6.            Metodo di Hsieh e Ou (1998)

Hsieh e Ou (1998) sulla base di un’analisi statistica di un certo numero di casi di scavi a cielo aperto in terreni a grana fine proposero un metodo empirico per la stima della forma del profilo dei cedimenti sia a mensola che concavo.

Il profilo a mensola (spandrel) è modellato con le seguenti equazioni (Figura 16):

v         0.6361        per      d  2

 

vmHe  (8)

^v   0.171 0.342           per      2  ^d  4         

_vm _He

Il profilo concavo è modellato con le seguenti equazioni (Figura 17):

vm v  Hd e      0.5           per      Hde  0.5

_vm v     53 H d    1.3    per      0.5  Hde  2 (9)

e

v     0.05 d    0.2         per      2  d  4

vm        H_e           He

Per entrambi i profili nel primo tratto, denominato zona di influenza primaria, fino ad una distanza

 d      

pari a due volte la profondità dello scavo ^_{ He}  ²_ ^_ , la curva ha una pendenza piuttosto elevata e,

_

se _vm è significativo, può determinare grandi distorsioni angolari negli edifici prossimi allo scavo. Per distanze maggiori e fino a quattro volte la profondità dello scavo, nella zona denominata di influenza secondaria la curva ha una pendenza molto minore e non è in genere pericolosa per gli

edifici.

d/H_e             d/H_e

 

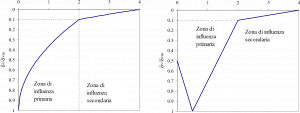
Figura 16 – Profilo dei cedimenti a mensola        Figura 17 – Profilo dei cedimenti concavo

Gli Autori presentarono anche numerosi esempi di casi reali in cui le misure sperimentali erano messe a confronto con le curve teoriche del loro metodo e di altri metodi di letteratura. Ad esempio nelle Figure 18 e 19 sono riportati due casi rispettivamente di profilo a mensola e di profilo concavo.

 

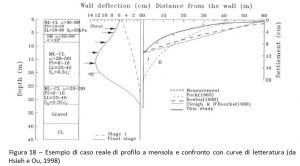
Figura 18 – Esempio di caso reale di profilo a mensola e confronto con curve di lettura (da Hsieh e Ou, 1998)

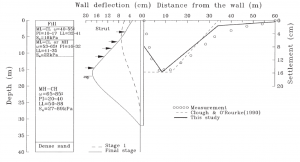
Figura 19 – Esempio di caso reale di profilo concavo e confronto con curve di letteratura (da Hsieh e Ou, 1998)

 

3.7.            Metodo di Bryson e Zapata‐Medina (2012)

Bryson e Zapata‐Medina (2012), sulla base di un estesa analisi parametrica condotta con un programma agli elementi finiti tridimensionale (PLAXIS 3D) implementando per il terreno una sofisticata legge costitutiva elasto‐plastica, proposero un metodo semi‐empirico di stima dei movimenti del terreno causati da scavi a cielo aperto in argilla. Le equazioni per la stima dei movimenti furono determinate con regressioni ai minimi quadrati sui risultati numerici, e validate su numerosi casi reali.

È introdotto un parametro denominato rapporto di rigidezza relativa, definito nel modo seguente:

R  E s  SH SV H  s He                                                           (10)

E         I          s_u

ove i simboli hanno il seguente significato:

Es	modulo di Young del terreno,
E	modulo di Young della parete,
I	momento di inerzia per unità di lunghezza della parete,
SH	interasse medio dei vincoli (tiranti o puntoni) in direzione orizzontale,
SV	interasse medio dei vincoli (tiranti o puntoni) in direzione verticale,
H	altezza totale della parete,
He	profondità di scavo,
s	peso di volume medio del terreno,
su	resistenza al taglio non drenata del terreno alla base dello scavo.

Lo spostamento laterale massimo della parete è espresso in funzione del parametro R e del fattore di sicurezza rispetto al sollevamento del fondo scavo FS determinato con l’equazione (7) di Ukritchon et al. (2003) (Figura 20):

hm % _ 0.275_FS0.9322 _R0.25850.0351FS^                                   (11)

H

Una relazione empirica, dedotta da un’analisi statistica dei dati sperimentali, fra gli spostamenti massimi orizzontale e verticale è la seguente (Figura 13):

0.7696

hm    0.9221 vm                                                                           (12)

H      H 

La migliore capacità previsionale del metodo proposto rispetto a quello di Clough et al. (1989) fu valutata dagli Autori confrontando le stime con i dati relativi ad alcuni casi reali descritti in letteratura (Figura 15).

Dall’analisi svolta gli Autori concludono che:

‐ per gli effetti 3‐D (non considerati da altri metodi) la rigidezza del sistema è molto più dipendente dall’interasse dei vincoli in direzione orizzontale che in direzione verticale,

‐ gli spostamenti laterali delle opere di sostegno in argille consistenti con un adeguato coefficiente di sicurezza rispetto al sollevamento del fondo scavo (FS) sono quasi indipendenti dalla rigidezza flessionale della parete,

‐ mentre per scavi in argilla di bassa e media consistenza con bassi valori di FS la rigidezza flessionale della parete gioca un ruolo importante nel comportamento del sistema.

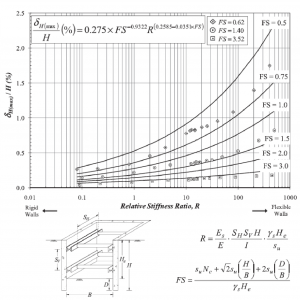
Figura 20 – Stima dello spostamento orizzontale massimo della parete vincolata di sostegno di uno scavo in argilla (Bryson e  Zapata‐Medina, 2012) Figura 21 – Relazione empirica fra massimi spostamenti orizzontali e verticali (Bryson e Zapata‐Medina, 2012)

 

4. Stima degli effetti tridimensionali

I metodi di calcolo all’equilibrio limite e a molle indipendenti, così come i metodi semi‐empirici di stima della deformata del muro diaframma e del profilo dei cedimenti si riferiscono a condizioni di deformazione piana. Solamente un metodo ed un modello di calcolo a elementi finiti tridimensionali è in grado di stimare l’effettivo stato di tensione e di deformazione di uno scavo tridimensionale.

Ou et al. (1996) svolsero un’analisi parametrica con un codice di calcolo agli elementi finiti tridimensionali per valutare gli effetti tridimensionali sulla deformata di diaframmi di sostegno di scavi di forma rettangolare (Figura 23). I risultati dello studio sono sintetizzati nel grafico di Figura 24, in cui, in funzione del rapporto fra i lati del rettangolo (B/L) e della distanza dall’angolo (d), si stima il valore del rapporto PSR (Plane Strain Ratio) fra il massimo spostamento orizzontale del muro in corrispondenza di una sezione posta a distanza d dall’angolo (_hm,d) e il massimo spostamento orizzontale del muro in condizioni di deformazione piana (_hm,ps).

 

5. Rischio di danno agli edifici

La realizzazione di uno scavo a cielo aperto o in sotterraneo può comportare un rischio di danneggiamento per gli edifici esistenti in prossimità o sovrastanti lo scavo.

In taluni casi (per fortuna “estremi”) l’esecuzione di uno scavo può determinare il crollo per ribaltamento di un edificio, come mostrato in Figura 24, le cui immagini si riferiscono al collasso di un edificio di 13 piani avvenuto a Shanghai (Cina) nel 2009. Il crollo dell’edificio, fondato su pali, fu causato dall’azione simultanea dello scavo da un lato e dell’accumulo del terreno scavato dal lato opposto (Chai et al., 2014).

Figura 24 – Collasso di un edificio come conseguenza di uno scavo a cielo aperto (da Chai et al., 2014)

Più frequentemente possono verificarsi danni alle strutture portanti o agli elementi architettonici portati (tramezzi, pavimentazioni, infissi, etc..) per eccessive deformazioni e/o spostamenti (Figura 25). L’entità del danno potenziale dipende da moltissimi fattori, quali la tipologia edilizia, la rigidezza della struttura, la tipologia e la profondità delle fondazioni, la distanza e la posizione dell’edificio rispetto allo scavo, le caratteristiche geometriche dello scavo, la struttura di sostegno, le condizioni geotecniche e idrauliche, la successione e la durata delle fasi di costruzione, etc.. Inoltre poiché la presenza degli edifici modifica il profilo dei cedimenti in campo libero, l’analisi del rischio dovrebbe comprendere uno studio di interazione terreno‐struttura. Pertanto un approccio puramente teorico non è quasi mai praticabile e occorre affidarsi a metodi semi‐empirici e a criteri e soglie di danno convenzionali.

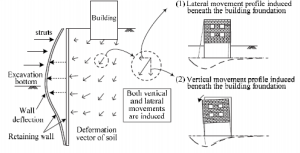
Figura 25 – Deformazioni del terreno e degli edifici in prossimità di uno scavo (Schuster et al., 2009)

Nelle Figure 26 e 27 (Burland et al., 2001)) sono graficamente rappresentati i parametri che descrivono i cedimenti assoluti e differenziali di un edificio: i punti A, B, C e D possono rappresentare plinti isolati di un sistema di fondazioni superficiali, ma anche punti appartenenti ad un muro, ad una trave o ad una platea di fondazione.

Con riferimento alle Figure 26 e 27 i parametri, e i relativi simboli, sono i seguenti:

S cedimento, ovvero spostamento massimo di un punto,

S_max, cedimento massimo (S_max = S_B),

S, cedimento differenziale, ovvero differenza fra i cedimenti di due punti,

S_max, cedimento differenziale massimo, (S_max = S_BD = S_B – S_D),

, rotazione ovvero pendenza rispetto all’orizzontale della retta congiungente due punti consecutivi,

_max, rotazione massima (_max = _AB = arctan(S_AB/L_AB)

 rotazione rigida, ovvero pendenza rispetto all’orizzontale della retta congiungente i due punti A e D di estremità ( = arctan(S_AD/L_AD),

 inflessione relativa, ovvero distanza del punto i (i = B, C), rispetto alla retta congiungente i due punti di estremità,

_max inflessione relativa massima (_max = _B),

/L rapporto d’inflessione, rapporto fra l’inflessione relativa e la lunghezza totale L = L_AD

 deformazione angolare, (positiva per concavità verso l’alto – sagging – e negativa per concavità verso il basso – hogging –), rappresenta la rotazione totale in un punto (_B = _AB + _BC);

 rotazione relativa o distorsione angolare, rotazione della retta congiungente due punti rispetto alla retta congiungente i punti di estremità (_AB = _AB + , _DC = _DC ‐ );

 

_h = (L₂‐L₁)/L deformazione orizzontale media.

 

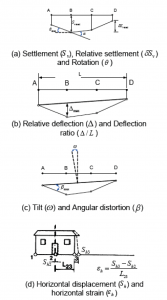
Figura 26 – Definizione delle deformazioni che possono interessare un edificio (Burland et al., 2001)

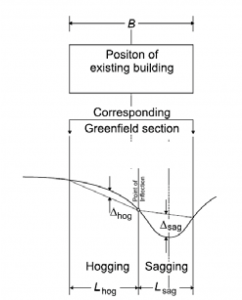Figura 27 – Definizione dei modi di deformazione “sagging” (concavità verso l’alto) e “hogging” (concavità verso il basso)

 

Esistono molti grafici e tabelle, proposti da vari Autori, che su base statistica indicano i valori ammissibili dei diversi parametri che definiscono i cedimenti assoluti e differenziali. A titolo di esempio, in Tabella 2, sono riportati alcuni dei valori della distorsione angolare limite suggeriti da Bjerrum (1963).

 

Tabella 2 ‐ Distorsioni angolari limite secondo Bjerrum (1962)

Categoria di danno potenziale       tan

Limite oltre il quale possono sorgere problemi in macchinari sensibili ai

1/750 cedimenti

Limite di pericolo per strutture reticolari     1/600

Limite di sicurezza per edifici in cui non si ammettono fessurazioni          1/500

Limite oltre il quale possono apparire le prime fessure nei muri di tam‐

1/300 ponamento e difficoltà nell’uso dei carri ponte

Limite oltre il quale possono essere visibili inclinazioni di edifici alti         1/250

Notevoli fessure in muri di tamponamento e muri portanti in laterizio.

Limite di sicurezza per muri portanti in laterizio con h/L<1/4.       1/150

Limite oltre il quale si devono temere danni strutturali negli edifici.

Polshin e Tokar (1957) studiarono l’effetto della geometria dell’edificio, rappresentata dal rapporto (L/H) in cui L è la distanza fra due giunti e H è l’altezza dell’edificio. Assumendo come valore di deformazione a trazione limite per la muratura di mattoni il valore 0.05%, conclusero che i valori limite di deformazione per edifici con struttura portante in muratura di mattoni, espressi in termini di rapporto d’inflessione (/L) valgono:

‐	Per concavità verso l’alto (“sagging”):	(L/H≤3)	(/L)max = 1/3300 – 1/2500
‐	Per concavità verso l’alto (“sagging”):	(L/H≥5)	(/L)max = 1/2000 – 1/1400

Secondo Rankin (1988) per gli edifici che subiscono rotazioni tan  210^3 e cedimenti assoluti S<1 cm il rischio di danneggiamento è trascurabile.

Un altro criterio di valutazione del rischio di fessurazione si basa sulla deformazione di trazione: secondo Boscardin e Cording (1989) le categorie di rischio sono riassunte in Tabella 3.

Una valutazione sommaria ma cautelativa del rischio di danneggiamento può essere svolta assumendo che gli edifici si adattino al profilo dei cedimenti in campo libero, come se fossero privi di peso e di rigidezza. Qualora il risultato di tale valutazione porti ad escludere o comunque a stimare basso il rischio di danneggiamento, l’analisi può considerarsi conclusa.

Secondo Burland e Wroth (1974) l’edificio può essere modellato con una trave omogenea che si deforma a flessione e a taglio seguendo il profilo dei cedimenti in campo libero (Figura 28), e può lesionarsi per flessione con deformazioni di trazione orizzontale o per taglio con deformazioni di trazione diagonali. Secondo gli Autori le soglie alle quali si formano le lesioni per taglio o per flessione nelle murature portanti di un edificio sono funzione della concavità, verso l’alto “sagging” o verso il basso “hogging”, del rapporto (L/H) e di un parametro di deformazione definito dal rapporto /(L _lim) (Figure 29 e 30).

 

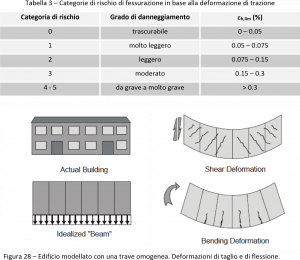
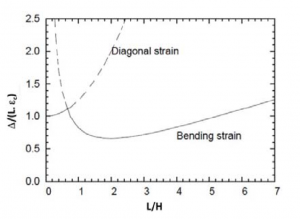
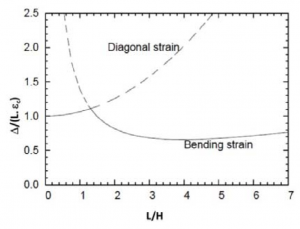
Figura 29 – Soglie di danno per conca‐ Figura 30 – Soglie di danno per concavità verso l’alto “sagging” di murature vità verso il basso “hogging” di muraportanti (Burland e Wroth, 1974) ture portanti (Burland e Wroth, 1974)

 

Boscardin e Cording (1989) dimostrarono che la deformazione orizzontale è molto influente sul livello di danno agli edifici e proposero un criterio basato sulle deformazioni principali.

Schuster et al. (2009) introdussero un nuovo parametro, detto Indice di Danno Potenziale (DPI), funzione della distorsione angolare  e della deformazione laterale _l nell’edificio, il cui valore è correlato con il livello di danno.

Per ridurre il rischio di danneggiamento possono eseguirsi opere di consolidamento preventivo e/o di mitigazione degli effetti. Esistono molte tecniche (ad es. iniezioni cementizie e/o chimiche, diaframmi di jet grouting, ombrelli di infilaggi, etc..) ma, a parte il costo elevato ed eventuali contro indicazioni, la loro efficacia può essere verificata solo in corso d’opera e potrebbe ridursi nel tempo per fenomeni viscosi e/o per degrado dei materiali.

È dunque molto importante prevedere un accurato sistema di monitoraggio che comprenda misure di subsidenza del terreno e dei fabbricati ubicati in prossimità dello scavo.

I risultati del monitoraggio devono essere confrontati con valori di soglia, di attenzione e di allarme definiti in fase progettuale. Le misurazioni sono necessarie per conoscere l’effettiva risposta del terreno in sito, verificare la corrispondenza con la previsione progettuale, e se necessario adeguare la progettazione in corso d’opera.

Occorre infine considerare il così detto “danno occulto”, ovvero la riduzione delle riserve di resistenza delle murature derivanti dalle variazioni dello stato tensionale e deformativo senza che siano superati i valori di resistenza a rottura e quindi senza che si siano manifestate lesioni visibili.

 

 

Riferimenti bibliografici

Bauer G.E. (1984) – Movements associated with the construction of a deep excavation. Proc. 3^rd Int. Conf. Ground Mov. And Structures, Cardiff, pp. 129‐156

Bjerrum L. (1963) – “Discussion”, Proc. of the European Conference on Soil Mechanics and Foundation Engineering, Vol. III, Wiesbaden, pp. 163

Boscardin M.D. e Cording E.G. (1989) – Building response to excavation‐induced settlement. J. Geotech. Engg., ASCE, 115 (1), pp. 1‐21

Bowles J.E. (1988) ‐ Foundation analysis and design. 4^th ed. McGraw‐Hill Book Company, New York.

Bryson L.S. e Zapata‐Medina D.G. (2012) – Method for estimating system stiffness for excavation support walls. Journal of Geotechnical and Geoenvirormental Engineering, ASCE, Vol. 138(9), pp. 1104‐1115

Burland J.B., Standing J.R. e Jardine F.M. (2001) – Building response to tunnelling. Case studies from construction of the Jubilee line extension. London Volume 1 Projects and Methods, CIRIA Special Publication 200. Thomas Telford, London

Burland J.B. e Wroth C.P. (1974) – Settlement of buildings and associated damage. Proc. of a Conference on Settlement of Structures. Cambridge, pp. 611‐654

Caspe M.S. (1966) ‐ Surface Settlement Adjacent to Braced Open Cuts. JSMFD, ASCE, vol. 92, SM 4, July, pp. 51‐59

Chai J., Shen S., Ding W., Zhu H. e Carter J. (2014) – Numerical investigation of the failure of a building in Shanghai, China. Computers and Geotechnics, 55, pp. 482‐493

Clough G.W. e O’Rourke T.D. (1990) ‐ Construction‐induced movements of in situ walls. Proceedings, Design and Performance of Earth Retaining Structures, ASCE Special Conference, Ithaca, New York, pp. 439–470.

Clough G.W., Smith E.M. e Sweeney B.P. (1989) ‐ Movement control of excavation support systems by iterative design. Foundation Engineering: Current Principles and practices, Vol.2, ASCE, New York, NY, 1989, pp869‐882.

Hsiao C.L. (2007) – Wall and ground movements in a braced excavation in clays and serviceability reliability of adjacent buildings. Ph.D. thesis, Clemson University

Hsieh P.‐G. e Ou C.‐Y. (1998) – Shape of ground surface settlement profiles caused by excavation. Canadian Geotechnical Journal, 35: 1004‐1017

Long M. (2001) ‐ Database for retaining wall and ground movements due to deep excavations. Journal of Geotechnical and Geoenvironmental Engineering, 127(3), 203–224.

Milligan G.W.E. (1983) ‐ Soil deformation near anchored sheet‐pile walls. Géotechnique, 33(1): 41 –

Ou C.Y. (2006) – Deep excavation. Theory and Practice. Taylor & Francis/Balkema

Ou C.Y., Chiou D.C. e Wu T.S. (1996) – Three‐dimensional finite element analysis of deep excavations, Journal of Geotechnical Engineering, ASCE, Vol. 122(5), pp. 337‐345

Ou C.Y., Liao J.T. e Lin H.D. (1998) – Performance of diaphragm wall constructed using top‐down method. Journal of Geotechnical and Geoenvironmental Engineering, ASCE, Vol. 124(9), pp. 798‐808

Ou C.Y. e Yang L.L. (2000) – Ground movement induced by the construction of diaphragm wall, Geotechnical Research Report No GT GT200005, Department of Construction Engineering, National Taiwan University of Science and Technology, Taipei, Taiwan, R.O.C.

Peck R.B. (1969) – Deep excavations and tunnelling in soft ground. State of the art report, Mexico city, State of the art volume, Proc. 7^th Int. Conf. SMFE, pp. 225‐290

Polshin D.E. e Tokar R.A. (1957) “Maximum allowable non‐uniform settlement of structures” Proc. of the 4^th Int. Conf. on Soil Mech. and Found. Engineering, Vol. 1, pp. 402‐405

Rankin W.J. (1988) – Ground movements resulting from urban tunnelling; prediction and effects.

Engineering geology of underground movement, Geological Society, Engineering Geology Special Publication, No 5, pp. 79‐92

Schuster M., Kung G.T., Juang C.H. e Hashash Y.M.A. (2009) – Simplified model for evaluating damage potential of buildings adjacent to a braced excavation. Journal of Geotechnical and Ge‐

oenvironmental Engineering, ASCE, Vol. 135(12), pp. 1823‐1835

Terzaghi K. (1943) ‐ Theoretical soil mechanics, John Wiley, New York

Ukritchon B., Whittle A.J. e Sloan S.W. (2003) – Undrained stability of braced excavations in clay. Journal of Geotechnical and Geoenvironmental Engineering, ASCE, Vol. 129(8), pp. 738‐755